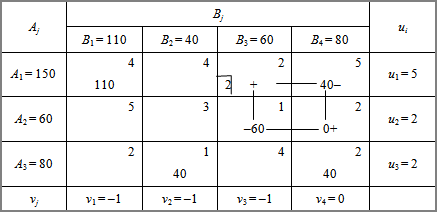Відмінності між версіями «Умова оптимальності опорного плану ТЗ»

Матеріал з Вікі ЦДУ
Перейти до: навігація, пошук
Рядок 18: Рядок 18:
  
 
[[Зображення:Транспортна таблиця.png]]
 
[[Зображення:Транспортна таблиця.png]]
 +
 +
Z = 4 * 110 + 5 * 40 + 1 * 60 + 1 * 40 + 2 * 40 = 820 ум. од.
 +
 +
Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п'яти, а (m + n - 1) = 3 + 4 - 1 = 6. Для подальшого розв'язування задачі необхідно в одну із порожніх клітинок записати "нульове перевезення" так, щоб не порушити опорності плану, тобто можна зайняти будь-яку вільну клітинку, яка не утворює замкненого циклу. Наприклад, заповнимо клітинку <math>A_2 B_4</math>. Тепер перший план транспортної задачі є невиродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.
 +
 +
На основі першої умови оптимальності <math>u_i + v_j = c_{ij}</math> складемо систему рівнянь для визначення потенціалів плану:
 +
 +
<math>\begin{cases}
 +
u_1 + v_1 = 4, \\
 +
u_1 + v_4 = 5, \\
 +
u_2 + v_3 = 1, \\
 +
u_2 + v_4 = 2, \\
 +
u_3 + v_2 = 1, \\
 +
u_3 + v_4 = 2.
 +
\end{cases}</math>
 +
 +
Записана система рівнянь є невизначеною, і один з її розв'язків дістанемо, якщо, наприклад, <math>v_4 = 0</math>. Тоді всі інші потенціали однозначно визначаються: <math>u_1 = 5, u_2 = 2, u_3 = 2, v_1 = -1, v_2 = -1, v_3 = -1.</math>
 +
 +
Далі згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності <math>u_i + v_j \leq c_{ij}</math> (для порожніх клітинок таблиці):
 +
 +
<math>\begin{array}
 +
A_1B_2: u_1 + v_2 = 5 + (-1) = 4 = 4; \\
 +
A_1B_3: u_1 + v_3 = 5 + (-1) = 4 > 2; \\
 +
A_2B_1: u_2 + v_1 = 2 + (-1) = 1 < 5; \\
 +
A_2B_2: u_2 + v_2 = 2 + (-1) = 1 < 3; \\
 +
A_3B_1: u_3 + v_1 = 2 + (-1) = 1 < 2; \\
 +
A_3B_3: u_3 + v_3 = 2 + (-1) = 1 < 4.
 +
\end{array}</math>
 +
 +
Умова оптимальності не виконується для клітинки <math>A_1B_3</math>. Порушення <math>\bigtriangleup_{13} = (u_1 + v_3) - c_{13} = 4 - 2 = 2</math> записуємо в лівому нижньому кутку відповідної клітинки.

Версія за 18:32, 10 травня 2012

Умова оптимальності опорного плану транспортної задачі

Опорний план перевіряють на оптимальність за допомогою потенціалів Неможливо розібрати вираз (невідома помилка): u_i 

та Неможливо розібрати вираз (невідома помилка): v_j
відповідно постачальників та споживачів.

Якщо для деякого опорного плану Неможливо розібрати вираз (невідома помилка): X^* = (x_{ij}^*) 

існують числа Неможливо розібрати вираз (невідома помилка): u_i
та Неможливо розібрати вираз (невідома помилка): v_j

, для яких виконується умова:

Неможливо розібрати вираз (невідома помилка): u_i + v_j = c_{ij}, x_{ij} > 0,


Неможливо розібрати вираз (невідома помилка): u_i + v_j \leq c_{ij}, x_{ij} = 0


для всіх Неможливо розібрати вираз (невідома помилка): i = \bar{1,m} 

та Неможливо розібрати вираз (невідома помилка): j = \bar{1,n}

, то він є оптимальним планом транспортної задачі.

Потенціали опорного плану визначаються із системи рівнянь Неможливо розібрати вираз (невідома помилка): u_i + v_j = c_{ij} , які записують для всіх заповнених клітинок транспортної таблиці.

Приклад перевірки транспортної задачі на оптимальний план

Нехай дана транспортна таблиця:

Транспортна таблиця.png

Z = 4 * 110 + 5 * 40 + 1 * 60 + 1 * 40 + 2 * 40 = 820 ум. од.

Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п'яти, а (m + n - 1) = 3 + 4 - 1 = 6. Для подальшого розв'язування задачі необхідно в одну із порожніх клітинок записати "нульове перевезення" так, щоб не порушити опорності плану, тобто можна зайняти будь-яку вільну клітинку, яка не утворює замкненого циклу. Наприклад, заповнимо клітинку Неможливо розібрати вираз (невідома помилка): A_2 B_4 . Тепер перший план транспортної задачі є невиродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.

На основі першої умови оптимальності Неможливо розібрати вираз (невідома помилка): u_i + v_j = c_{ij} 

складемо систему рівнянь для визначення потенціалів плану:

Неможливо розібрати вираз (невідома помилка): \begin{cases} u_1 + v_1 = 4, \\ u_1 + v_4 = 5, \\ u_2 + v_3 = 1, \\ u_2 + v_4 = 2, \\ u_3 + v_2 = 1, \\ u_3 + v_4 = 2. \end{cases}


Записана система рівнянь є невизначеною, і один з її розв'язків дістанемо, якщо, наприклад, Неможливо розібрати вираз (невідома помилка): v_4 = 0 . Тоді всі інші потенціали однозначно визначаються: Неможливо розібрати вираз (невідома помилка): u_1 = 5, u_2 = 2, u_3 = 2, v_1 = -1, v_2 = -1, v_3 = -1.


Далі згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності Неможливо розібрати вираз (невідома помилка): u_i + v_j \leq c_{ij} 

(для порожніх клітинок таблиці):

Неможливо розібрати вираз (невідома помилка): \begin{array} A_1B_2: u_1 + v_2 = 5 + (-1) = 4 = 4; \\ A_1B_3: u_1 + v_3 = 5 + (-1) = 4 > 2; \\ A_2B_1: u_2 + v_1 = 2 + (-1) = 1 < 5; \\ A_2B_2: u_2 + v_2 = 2 + (-1) = 1 < 3; \\ A_3B_1: u_3 + v_1 = 2 + (-1) = 1 < 2; \\ A_3B_3: u_3 + v_3 = 2 + (-1) = 1 < 4. \end{array}


Умова оптимальності не виконується для клітинки Неможливо розібрати вираз (невідома помилка): A_1B_3 . Порушення Неможливо розібрати вираз (невідома помилка): \bigtriangleup_{13} = (u_1 + v_3) - c_{13} = 4 - 2 = 2 

записуємо в лівому нижньому кутку відповідної клітинки.
Отримано з https://wiki.cusu.edu.ua/index.php?title=Умова_оптимальності_опорного_плану_ТЗ&oldid=67698