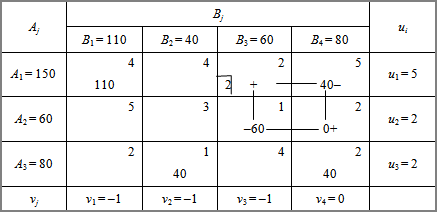Відмінності між версіями «Умова оптимальності опорного плану ТЗ»
Матеріал з Вікі ЦДУ
(Створена сторінка: == Умова оптимальності опорного плану транспортної задачі == Опорний план перевіряють на ...) |
|||
| Рядок 6: | Рядок 6: | ||
<math>u_i + v_j = c_{ij}, x_{ij} > 0,</math> | <math>u_i + v_j = c_{ij}, x_{ij} > 0,</math> | ||
| − | <math>u_i + v_j \ | + | |
| + | <math>u_i + v_j \leq c_{ij}, x_{ij} = 0</math> | ||
для всіх <math>i = \bar{1,m}</math> та <math>j = \bar{1,n}</math>, то він є оптимальним планом транспортної задачі. | для всіх <math>i = \bar{1,m}</math> та <math>j = \bar{1,n}</math>, то він є оптимальним планом транспортної задачі. | ||
Версія за 18:15, 10 травня 2012
Умова оптимальності опорного плану транспортної задачі
Опорний план перевіряють на оптимальність за допомогою потенціалів Неможливо розібрати вираз (невідома помилка): u_i
та Неможливо розібрати вираз (невідома помилка): v_j відповідно постачальників та споживачів.
Якщо для деякого опорного плану Неможливо розібрати вираз (невідома помилка): X^* = (x_{ij}^*)
існують числа Неможливо розібрати вираз (невідома помилка): u_i та Неможливо розібрати вираз (невідома помилка): v_j
, для яких виконується умова:
Неможливо розібрати вираз (невідома помилка): u_i + v_j = c_{ij}, x_{ij} > 0,
Неможливо розібрати вираз (невідома помилка): u_i + v_j \leq c_{ij}, x_{ij} = 0
для всіх Неможливо розібрати вираз (невідома помилка): i = \bar{1,m}
та Неможливо розібрати вираз (невідома помилка): j = \bar{1,n}
, то він є оптимальним планом транспортної задачі.
Потенціали опорного плану визначаються із системи рівнянь Неможливо розібрати вираз (невідома помилка): u_i + v_j = c_{ij} , які записують для всіх заповнених клітинок транспортної таблиці.
Приклад перевірки транспортної задачі на оптимальний план
Нехай дана транспортна таблиця: