Відмінності між версіями «Методи відтинання. Метод Гоморі»
Tenatin (обговорення • внесок) (Створена сторінка: Метод відсікання. алгоритм Гоморі Загальна задача лінійного дискретного цілочисельног...) |
Tenatin (обговорення • внесок) |
||
| Рядок 19: | Рядок 19: | ||
Завдання не буде мати повністю цілочисельного рішення, якщо зустрінеться в симплекс-таблице рівняння таке, що βi дробове число, а αij-цілі. | Завдання не буде мати повністю цілочисельного рішення, якщо зустрінеться в симплекс-таблице рівняння таке, що βi дробове число, а αij-цілі. | ||
| − | Пример решения методом Гомори.<br> | + | ''Пример решения методом Гомори.''<br> |
Решить задачу ЛП max: Z = 3 x1 + x 2 <br> | Решить задачу ЛП max: Z = 3 x1 + x 2 <br> | ||
при ограничениях: 3x1 – 2x2 ≤3 <br> | при ограничениях: 3x1 – 2x2 ≤3 <br> | ||
Версія за 18:09, 10 травня 2012
Метод відсікання. алгоритм Гоморі
Загальна задача лінійного дискретного цілочисельного програмування має вигляд:
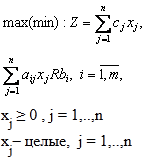
Задача називається повністю целочисленной завданням лінійного програмування, тому що на всі змінні покладено умова цілочисельності.
Коли ця умова стосується лише деяким змінним, завдання називається частково целочисленной.
Нехай дана задача повністю цілочисельного лінійного програмування. Алгоритм методу відсікань складається з наступних етапів:
1) вирішується ЗЛП з відкинутими умовою цілочисельності; якщо вона не розв'язана, то завдання теж рішення не має;
2) якщо умова цілочисельності виконується по всім змінним, то знайдене рішення є рішення задачі;
3) інакше будується додаткове відсікають обмеження, включається в систему обмежень і на етап 1.
Для рішення повністю целочисленной завдання ЛП Гоморі запропоновано робити кожен раз на етапі 3 додаткове обмеження для нецілої змінної з найбільшою дробовою частиною.
Припустимо, що завдання з відкинутим умовою цілочисельності вирішена. Розглянемо i-й рядок оптимальної симплексного таблиці, якій відповідає неціле рішення β i базисної змінної xi Нехай R - безліч індексів j, які відповідають небазисним змінним. Тоді мінлива xi може бути виражена через небазисних змінних xj:
![]() - не целое.
Обозначим наибольшую целую часть числа a, его не превосходящую, через [a], ( a≥[a]), а дробную положительную часть – через {a} Очевидно a = [a] + {a}. Например, если a=4,7 то [a] = 4, {a} = 0,7, если a =-8,6, то [a] = -9, {a} = 0,4.
Выразим базисную переменную xi в виде суммы целой и дробной частей.
- не целое.
Обозначим наибольшую целую часть числа a, его не превосходящую, через [a], ( a≥[a]), а дробную положительную часть – через {a} Очевидно a = [a] + {a}. Например, если a=4,7 то [a] = 4, {a} = 0,7, если a =-8,6, то [a] = -9, {a} = 0,4.
Выразим базисную переменную xi в виде суммы целой и дробной частей.
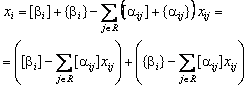 Вираз в лівих круглих дужках (4.6) ціле число, і щоб xj було цілим, необхідно, щоб вираження у правих круглих дужках (4.6) теж було цілим. коли вираз
Вираз в лівих круглих дужках (4.6) ціле число, і щоб xj було цілим, необхідно, щоб вираження у правих круглих дужках (4.6) теж було цілим. коли вираз
 буде цілим? Так як 0 ≤
буде цілим? Так як 0 ≤ ![]() то Li буде цілим числом, якщо
то Li буде цілим числом, якщо  тобто
тобто  .Співвідношення визначає правильне відсікання Гоморі.
Завдання не буде мати повністю цілочисельного рішення, якщо зустрінеться в симплекс-таблице рівняння таке, що βi дробове число, а αij-цілі.
.Співвідношення визначає правильне відсікання Гоморі.
Завдання не буде мати повністю цілочисельного рішення, якщо зустрінеться в симплекс-таблице рівняння таке, що βi дробове число, а αij-цілі.
Пример решения методом Гомори.
Решить задачу ЛП max: Z = 3 x1 + x 2
при ограничениях: 3x1 – 2x2 ≤3
-5 x1 – 4x 2 ≤ -10;
2 x1 + x 2 ≤ 5;
x1, x 2 ≥ 0
x1, x 2 – целые.
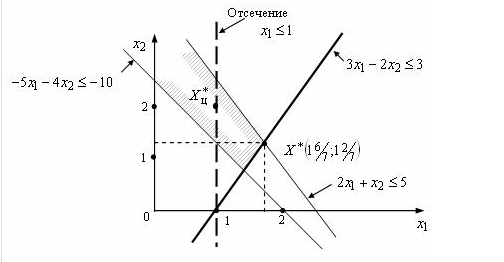
Рис. - Геометрична інтерпретація відсікання Гоморі
по теме Справочники, руководства Решение задач в онлайн режиме
Метод отсечения. Алгоритм Гомори
Общая задача линейного дискретного целочисленного программирования имеет вид: xj ≥ 0 , j = 1,..,n xj– целые, j = 1,..,n
Задача называется полностью целочисленной задачей линейного программирования, т.к. на все переменные положено условие целочисленности . Когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной.
Пусть дана задача полностью целочисленного линейного программирования . Алгоритм метода отсечений состоит из следующих этапов:
1) решается ЗЛП с отброшенными условием целочисленности; если она не разрешима, то задача тоже решения не имеет;
2) если условие целочисленности выполняется по всем переменным, то найденное решение есть решение задачи;
3) иначе строится дополнительное отсекающее ограничение, включается в систему ограничений и на этап 1.
Для решения полностью целочисленной задачи ЛП Гомори предложено делать каждый раз на этапе 3 дополнительное ограничение для нецелой переменной с наибольшей дробной частью.
Предположим, что задача с отброшенным условием целочисленности решена. Рассмотрим i-ю строку оптимальной симплексной таблицы, которой соответствует нецелое решение β i базисной переменной xi Пусть R – множество индексов j, которые соответствуют небазисным
переменным. Тогда переменная xi может быть выражена через небазисные переменные xj:
β i – нецелое.
Обозначим наибольшую целую часть числа a, его не превосходящую, через [a], ( a≥[a]), а дробную положительную часть – через {a} Очевидно a = [a] + {a}. Например, если a=4,7 то [a] = 4, {a} = 0,7, если a =-8,6, то [a] = -9, {a} = 0,4.
Выразим базисную переменную xi в виде суммы целой и дробной частей.
Выражение в левых круглых скобках целое число, и чтобы xj было целым, необходимо, чтобы выражение в правых круглых скобках тоже было целым. Когда выражение будет целым? Так как 0 ≤ {βi}≤1, а то Li будет целым числом, если т.е.
Соотношение определяет правильное отсечение Гомори. Задача не будет иметь полностью целочисленного решения, если встретится в симплекс-таблице уравнение такое, что βi дробное число, а αij –целые.
Пример решения методом Гомори. Решить задачу ЛП max: Z = 3 x1 + x 2 при ограничениях: 3x1 – 2x2 ≤3 -5 x1 – 4x 2 ≤ -10; 2 x1 + x 2 ≤ 5; x1, x 2 ≥ 0 x1, x 2 – целые. Без учета целочисленности оптимальной симплекс-таблицей будет следующая табл. Рис. - Геометрическая интерпретация отсечения Гомори
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Поскольку в правой части присутствуют отрицательные значения, умножим соответствующие строки на (-1).
Определим максимальное значение целевой функции F(X) = 3x1 + x2 при следующих условиях-ограничений.
3x1 - 2x2≤3
5x1 + 4x2≥10
2x1 + x2≤5
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
3x1-2x2 + 1x3 + 0x4 + 0x5 = 3
5x1 + 4x2 + 0x3-1x4 + 0x5 = 10
2x1 + 1x2 + 0x3 + 0x4 + 1x5 = 5
Введем искусственные переменные x.
3x1-2x2 + 1x3 + 0x4 + 0x5 + 0x6 = 3
5x1 + 4x2 + 0x3-1x4 + 0x5 + 1x6= 10
2x1 + 1x2 + 0x3 + 0x4 + 1x5 + 0x6= 5
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = 3x1+x2 - Mx6 => max
Из уравнений выражаем искусственные переменные:
x6 = 10-5x1-4x2+x4
которые подставим в целевую функцию:
F(X) = (3+5M)x1+(1+4M)x2+(-1M)x4+(-10M) => max
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
 Вирішимо систему рівнянь щодо базисних змінних:
x3, x6, x5,
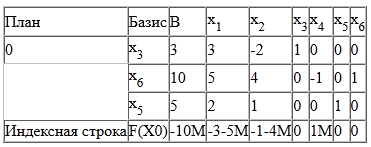
Вважаючи, що вільні змінні рівні 0, отримаємо перший опорний план:
X1 = (0,0,3,0,5,10)
Вирішимо систему рівнянь щодо базисних змінних:
x3, x6, x5,
Вважаючи, що вільні змінні рівні 0, отримаємо перший опорний план:
X1 = (0,0,3,0,5,10)
Переходимо до основного алгоритму симплекс-метода.
Ітерація № 0.
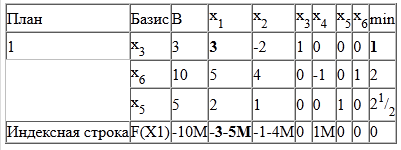
Поточний опорний план неоптимальний, тому що в індексному рядку знаходяться негативні коефіцієнти.
В якості ведучого виберемо стовпець, відповідний змінної x1, так як це найбільший коефіцієнт.
Обчислимо значення Di по рядках як частка від ділення:
і з них виберемо найменше:
min (3: 3, 10: 5, 5: 2) = 1
Отже, 1-а рядок є провідною.
Ітерація № 1.
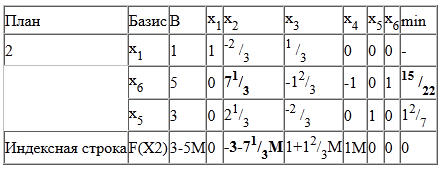
Поточний опорний план неоптимальний, тому що в індексному рядку знаходяться негативні коефіцієнти.
В якості ведучого виберемо стовпець, відповідний змінної x2, так як це найбільший коефіцієнт.
Обчислимо значення Di по рядках як частка від ділення:
і з них виберемо найменше:
min (-, 5: 71/3, 3: 21/3) = 15/22
Отже, 2-ий рядок є провідною.
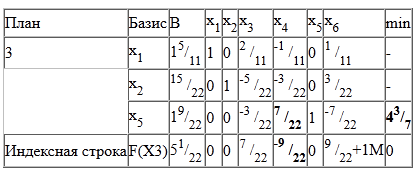
Ітерація № 2.
Поточний опорний план неоптимальний, тому що в індексному рядку знаходяться негативні коефіцієнти.
В якості ведучого виберемо стовпець, відповідний змінної x4, так як це найбільший коефіцієнт.
Обчислимо значення Di по рядках як частка від ділення:
і з них виберемо найменше:
min (-, -, 19/22: 7/22) = 43/7
Отже, 3-а рядок є провідною.
Кінець ітерацій: знайдений оптимальний план
Остаточний варіант симплекс-таблиці:
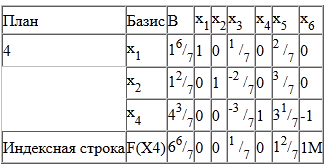 Оптимальний план можна записати так:
x1 = 16/7
x2 = 12/7
x4 = 43/7
F (X) = 3 • 16/7 + 1 • 12/7 = 66/7
В отриманому оптимальному плані присутні дробові числа.
По 1-у рівняння зі змінною x1, що отримала нецілочисельне значення в оптимальному плані з найбільшою дробовою частиною 6/7, складаємо додаткове обмеження:
q1 - q11 • x1 - q12 • x2 - q13 • x3 - q14 • x4 - q15 • x5 - q16 • x6 ≤ 0
q1 = b1 - [b1] = 16/7 - 1 = 6/7
q11 = a11 - [a11] = 1 - 1 = 0
q12 = a12 - [a12] = 0 - 0 = 0
q13 = a13 - [a13] = 1/7 - 0 = 1/7
q14 = a14 - [a14] = 0 - 0 = 0
q15 = a15 - [a15] = 2/7 - 0 = 2/7
q16 = a16 - [a16] = 0 - 0 = 0
Додаткове обмеження має вигляд:
6/7-1/7x3-2/7x5 ≤ 0
Перетворимо отримане нерівність в рівняння:
6/7-1/7x3-2/7x5 + x7 = 0
коефіцієнти якого введемо додаткової рядком в оптимальну симплексних таблицю.
Оптимальний план можна записати так:
x1 = 16/7
x2 = 12/7
x4 = 43/7
F (X) = 3 • 16/7 + 1 • 12/7 = 66/7
В отриманому оптимальному плані присутні дробові числа.
По 1-у рівняння зі змінною x1, що отримала нецілочисельне значення в оптимальному плані з найбільшою дробовою частиною 6/7, складаємо додаткове обмеження:
q1 - q11 • x1 - q12 • x2 - q13 • x3 - q14 • x4 - q15 • x5 - q16 • x6 ≤ 0
q1 = b1 - [b1] = 16/7 - 1 = 6/7
q11 = a11 - [a11] = 1 - 1 = 0
q12 = a12 - [a12] = 0 - 0 = 0
q13 = a13 - [a13] = 1/7 - 0 = 1/7
q14 = a14 - [a14] = 0 - 0 = 0
q15 = a15 - [a15] = 2/7 - 0 = 2/7
q16 = a16 - [a16] = 0 - 0 = 0
Додаткове обмеження має вигляд:
6/7-1/7x3-2/7x5 ≤ 0
Перетворимо отримане нерівність в рівняння:
6/7-1/7x3-2/7x5 + x7 = 0
коефіцієнти якого введемо додаткової рядком в оптимальну симплексних таблицю.
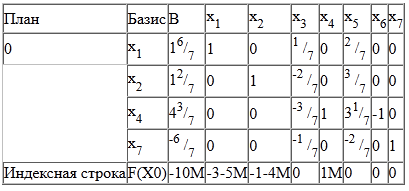
План 0 в симплексного таблиці є псевдопланом, тому визначаємо провідні рядок і стовпець.
Серед негативних значень базисних змінних вибираємо найбільший по модулю.
Провідною буде 4-й рядок, а змінну x7 слід вивести з базису.
У рядок θ заносимо наступні величини:
[-; -; 1/7: -1 / 7; -; 12/7: -2 / 7; -; -;] = [-; -; -1; -; -41 / 2; -; -; ]
Мінімальне значення θ відповідає 3-му стовпцю, тобто змінну x3 необхідно ввести в базис.
На перетині провідних рядка і стовпця знаходиться дозволяє елемент (РЕ), рівний -1 / 7.
Виконуємо перетворення симплексного таблиці методом Жордана-Гаусса.
Уявімо розрахунок кожного елемента у вигляді таблиці:
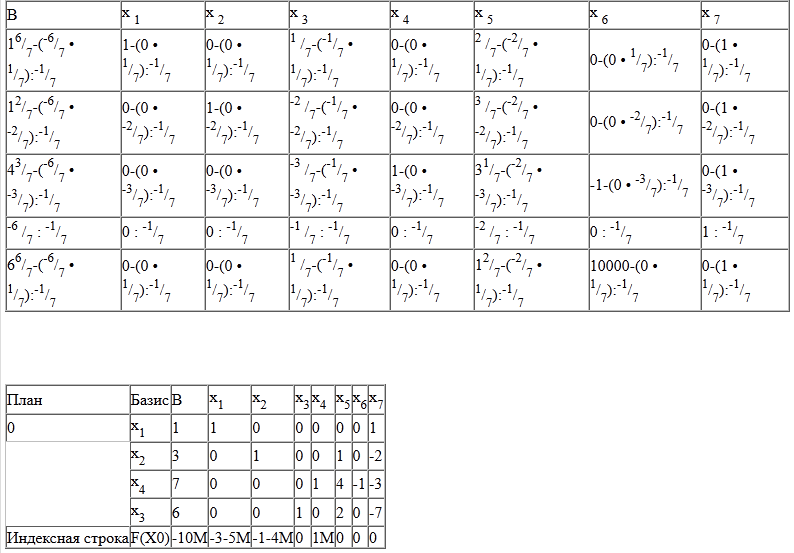
Рішення вийшло цілочисловим. Немає необхідності застосовувати метод Гоморі.
Оптимальний цілочисельний план можна записати так:
x1 = 1
x2 = 3
x4 = 7
x3 = 6
F(X) = 6
