Відмінності між версіями «Випадок виродження опорного плану ТЗ»
(Створена сторінка: Опорний план транспортної задачі, як зазначалося раніше, має містити не більше ніж ''(m+n-1)''...) |
|||
| Рядок 11: | Рядок 11: | ||
Таблиця 1.1 | Таблиця 1.1 | ||
| + | |||
| + | |||
| + | Перевіримо, чи є отриманий опорний план виродженим. Кількість постачальників ''m=4'', а кількість споживачів ''n=4''. Для невиродженого опорного плану кількість заповнених клітин таблиці 1.1 має дорівнювати ''m+n-1=4+3-1=6''. У наведеному опорному плані кількість заповнених клітин на одну менше (п’ять), отже, він вироджений. Позбудемося виродженості опорного плану введенням нульової поставки в одну з пустих клітин. Враховуючи необхідність збереження ациклічності опорного плану, не можна заповнювати клітини <math>A_{2\, }B_{1}</math> та <math>A_{4\, }B_{1}</math>, оскільки це призведе до утворення циклів, які зображені в табл. 1.2 та 1.3. | ||
| + | |||
| + | |||
| + | [[Файл:Табл._2.2.png]] | ||
| + | |||
| + | Таблиця 1.2 | ||
| + | |||
| + | |||
| + | [[Файл:Табл._2.3.png]] | ||
| + | |||
| + | Таблиця 1.3 | ||
| + | |||
| + | |||
| + | Очевидно введення нульової поставки в будь-яку іншу пусту клітинку не дає змоги утворити цикл. Отже, можна заповнити нулем одну з клітин <math>A_{1\, }B_{3}</math>, <math>A_{2\, }B_{3}</math>, <math>A_{3\, }B_{1}</math>, <math>A_{3\, }B_{2}</math>, <math>A_{4\, }B_{3}</math>. Наприклад, виберемо клітину <math>A_{3\, }B_{2}</math>. | ||
| + | |||
| + | |||
| + | [[Файл:Табл._2.4.png]] | ||
| + | |||
| + | Таблиця 1.4 | ||
| + | |||
| + | |||
| + | Зазначимо, що необхідність введення нульової поставки є очевиднішою на наступних етапах розв’язування транспортної задачі. | ||
| + | |||
| + | =='''Література'''== | ||
| + | |||
| + | Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. - К.: КНЕУ, 2003. - 452 с. | ||
Поточна версія на 19:47, 4 травня 2012
Опорний план транспортної задачі, як зазначалося раніше, має містити не більше ніж (m+n-1) відмінних від нуля компонент. Якщо їх кількість дорівнює (m+n-1) то такий опорний план називають невиродженим. Якщо ж кількість додатних компонент менша ніж (m+n-1), то опорний план є виродженим. Вироджений план може виникати не лише за побудови опорного плану, але і при його перетвореннях у процесі знаходження оптимального плану.
Найчастіше, щоб позбутися виродженості опорного плану, в деякі клітини таблиці транспортної задачі в необхідній кількості вводять нульові постачання. Обсяги запасів постачальників і потреби споживачів після цього не змінюються, однак клітини зі значенням «нуль» вважаються заповненими.
Головною умовою при введенні нульової поставки є збереження необхідної і достатньої умови опорності плану транспортної задачі — його ациклічності. Клітина має вибиратись у такий спосіб, щоб неможливо було побудувати замкнений цикл.
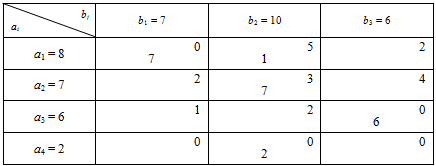
Нехай маємо такі умови транспортної задачі та початковий опорний план, що подані в табл. 1.1.
Таблиця 1.1
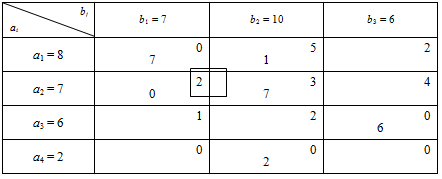
Перевіримо, чи є отриманий опорний план виродженим. Кількість постачальників m=4, а кількість споживачів n=4. Для невиродженого опорного плану кількість заповнених клітин таблиці 1.1 має дорівнювати m+n-1=4+3-1=6. У наведеному опорному плані кількість заповнених клітин на одну менше (п’ять), отже, він вироджений. Позбудемося виродженості опорного плану введенням нульової поставки в одну з пустих клітин. Враховуючи необхідність збереження ациклічності опорного плану, не можна заповнювати клітини Неможливо розібрати вираз (невідома помилка): A_{2\, }B_{1}
та Неможливо розібрати вираз (невідома помилка): A_{4\, }B_{1}
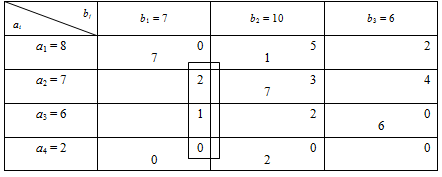
, оскільки це призведе до утворення циклів, які зображені в табл. 1.2 та 1.3.
Таблиця 1.2
Таблиця 1.3
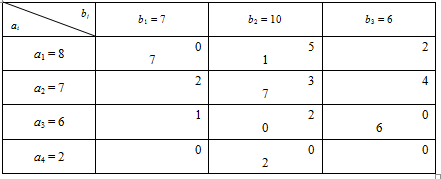
Очевидно введення нульової поставки в будь-яку іншу пусту клітинку не дає змоги утворити цикл. Отже, можна заповнити нулем одну з клітин Неможливо розібрати вираз (невідома помилка): A_{1\, }B_{3}
, Неможливо розібрати вираз (невідома помилка): A_{2\, }B_{3}
, Неможливо розібрати вираз (невідома помилка): A_{3\, }B_{1}
, Неможливо розібрати вираз (невідома помилка): A_{3\, }B_{2}
, Неможливо розібрати вираз (невідома помилка): A_{4\, }B_{3}
. Наприклад, виберемо клітину Неможливо розібрати вираз (невідома помилка): A_{3\, }B_{2}
.
Таблиця 1.4
Зазначимо, що необхідність введення нульової поставки є очевиднішою на наступних етапах розв’язування транспортної задачі.
Література
Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. - К.: КНЕУ, 2003. - 452 с.