Відмінності між версіями «Метод штучного базису»
| (не показано 5 проміжних версій цього учасника) | |||
| Рядок 77: | Рядок 77: | ||
| − | + | == Приклад == | |
<center><math>max Z\ =\ 8x_{1} +10x_{2} -5x_{4}</math></center> | <center><math>max Z\ =\ 8x_{1} +10x_{2} -5x_{4}</math></center> | ||
| Рядок 111: | Рядок 111: | ||
Зауважимо, що нерівність типу «≥» перетворюємо у рівняння введенням у ліву частину обмеження додаткової змінної зі знаком «–». | Зауважимо, що нерівність типу «≥» перетворюємо у рівняння введенням у ліву частину обмеження додаткової змінної зі знаком «–». | ||
| − | Система містить лише два одиничні вектори | + | Система містить лише два одиничні вектори <math>\vec{{A}}_{5} </math> та <math>\vec{{A}}_{6} </math> , а базис у тривимірному просторі має складатися з трьох одиничних векторів. Ще один одиничний вектор можна дістати, увівши в третє обмеження з |
коефіцієнтом +1 штучну змінну х8, якій від-повідатиме одиничний вектор <math>\vec{{A}}_{8} = \begin{pmatrix} 0 \\ 0 \\1 \end{pmatrix}</math> | коефіцієнтом +1 штучну змінну х8, якій від-повідатиме одиничний вектор <math>\vec{{A}}_{8} = \begin{pmatrix} 0 \\ 0 \\1 \end{pmatrix}</math> | ||
| + | |||
| + | Тепер можемо розглянути розширену задачу лінійного програмування: | ||
| + | |||
| + | <center><math> | ||
| + | maxZ\ =\ 8x_{1} +10x_{2} -5x_{4} +0x_{5} +0x_{6} -Mx_{8} | ||
| + | </math></center> | ||
| + | |||
| + | |||
| + | <center><math>\left\{ {\begin{array}{l} | ||
| + | 2x_{1} +3x_{2} +4x_{3} +2x_{4} +x_{5} =450; \\ | ||
| + | 3x_{1} +2x_{2} +x_{3} +2x_{4} +x_{6} =380; \\ | ||
| + | x_{3} -x_{7} +x_{8} =9; \\ | ||
| + | \end{array}} \right. | ||
| + | </math></center> | ||
| + | |||
| + | |||
| + | <center><math>x_{j} \ge 0,\,\,\,\,\,\,j\ge \overline {1,8} .</math></center> | ||
| + | |||
| + | |||
| + | На відміну від додаткових змінних штучна змінна х8 має в ці-льовій функції Z коефіцієнт +М (для задачі на min) або –М (для задачі на max), де М — досить велике додатне число. | ||
| + | У розширеній задачі базисними змінними є х5, х6, х8, а решта змінних вільні. Початковий опорний план задачі такий | ||
| + | |||
| + | <center><math>\begin{array}{c} | ||
| + | X_{0} =(0;\,\,0;\,\,0;\,\,0;\,\,450;\,\,380;\,\,0;\,\,9), \\ | ||
| + | Z_{0} =8\cdot 0+10\cdot 0+0\cdot 0-5\cdot 0+0\cdot 450+0\cdot 380+0\cdot | ||
| + | 0-M\cdot 9=-9M. \\ | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | |||
| + | <center>Складемо першу симплексну таблицю цієї задачі:</center> | ||
| + | |||
| + | |||
| + | <center>[[Зображення:M_OPT_T1.png]]</center> | ||
| + | |||
| + | |||
| + | Розраховуючи оцінки першого опорного плану, дістаємо: | ||
| + | Z0 = –9M; Z1 – с1 = –8; Z2 – с2 = –10, Z3 – с3 = –М і т. д. Отже, ми отримуємо оцінки двох видів: одні з них містять М, а інші є звичайними числами. Тому для зручності розділимо оцінковий рядок на два. У перший оцінковий рядок будемо записувати звичайні числа, а в другий — числа з коефіцієнтом М. | ||
| + | Оцінки першого плану не задовольняють умову оптимальності, і тому він є неоптимальним. Виконуємо перехід до наступного опорно-го плану задачі. Після першої ітерації з базису виведена штучна змінна х8. Дальше розв’язування продовжуємо за алгоритмом симплексного методу. | ||
| + | |||
| + | Наступні кроки розв’язування задачі наведені у загальній таблиці: | ||
| + | |||
| + | |||
| + | <center>[[Зображення:M_OPT_T2.png]]</center> | ||
| + | |||
| + | Оптимальним планом задачі є вектор: | ||
| + | <center><math>X^{\mathrm{\ast }} \quad = (57; 100; 9; 0; 0; 0; 0),</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\max Z=8\cdot 57+10\cdot 100+0\cdot 9-5\cdot 0=1456.</math></center> | ||
== Література == | == Література == | ||
http://fingal.com.ua/content/view/479/76/1/0/ | http://fingal.com.ua/content/view/479/76/1/0/ | ||
Поточна версія на 18:22, 4 травня 2012
Метод штучного базису застосовується в тих випадках коли система обмежень задачі лінійного програмування не містить одиничну матрицю порядку m.
Розглянемо задачу лінійного програмування:
Отримаємо одиничну матрицю додаванням штучних змінних
Неможливо розібрати вираз (невідома помилка): x_{n+i} \ge 0\;\,\,\,(i=\overline {1,m} )
лише в ті рівняння, які не розв’язані відносно базисних змінних.
Нехай штучну змінну введено у кожне рівняння:
область допустимих розв’язків задачі розширилась.
Задача з даною системою обмежень називається розширеноб, або М-задачею
Розв’язок розширеної задачі збігатиметься з розв’язком початкової лише за умови, що всі введені штучні змінні в оптимальному плані задачі будуть виведені з базису, тобто дорівнюватимуть нулеві
Для того, щоб у результаті процедур симплексних перетворень виключалися з базису штучні змінні, потрібно ввести їх у цільову функцію з великими від’ємними коефіцієнтами. Нехай величина М є достатньо великим за модулем числом. Цільова функція для задачі максимізації (мінімізації):
Якого б малого значення не набувала відповідна коефіцієнту штучна змінна Неможливо розібрати вираз (невідома помилка): x_{n+i}
, значення цільової функції
Неможливо розібрати вираз (невідома помилка): F^{\ast }
буде від’ємним для задачі на максимум та додатним для задачі на мінімум і водночас значним за модулем. Тому процедура симплексного методу одразу вилучає відповідні змінні з базису і забезпечує знаходження плану, в якому всі штучні змінні
Неможливо розібрати вираз (невідома помилка): x_{n+i} =0\;\left( {\,i=\overline {1,m} } \right)
Якщо в оптимальному плані розширеної задачі існує хоча б одне значення Неможливо розібрати вираз (невідома помилка): x_{n+i} >0
, то це означає, що початкова задача не має розв’язку, тобто система обмежень несумісна.
Для розв’язання розширеної задачі за допомогою симплексних таблиць зручно використовувати таблиці, оцінкові рядки яких поділені на дві частини-рядки. Тоді в (m+2)-му рядку записують коефіцієнти з М, а в (m+1)-му — ті, які не містять М. Вектор, який підлягає включенню до базису, визначають за (m+2)-м рядком. Ітераційний процес по (m+2)-му рядку проводять до повного виключення всіх штучних змінних з базису, потім процес визначення оптимального плану продовжують за (m+1)-им рядком.
Взаємозв’язок між розв’язками початкової та розширеної задач лінійного програмування не є очевидним і визначається такою теоремою.
Теорема
Якщо в оптимальному плані Неможливо розібрати вираз (невідома помилка): \mathord X _{opt} =(x_{1} ,\;x_{2} ,...,\;x_{n} ,\,0,\,...,\;0)
розширеної задачі штучні змінні Неможливо розібрати вираз (невідома помилка): x_{n+i} =0,\;\,\,(i=1,\;2,\;...,\;m)
то план Неможливо розібрати вираз (невідома помилка): X_{opt} =(x_{1}~ ,x_{2} ,...,~x_{n} )
є оптимальним планом початкової задачі.
Приклад
Застосовуючи для розв’язування поставленої задачі симплекс-метод, спочатку запишемо систему обмежень у канонічній формі:
Зауважимо, що нерівність типу «≥» перетворюємо у рівняння введенням у ліву частину обмеження додаткової змінної зі знаком «–». Система містить лише два одиничні вектори Неможливо розібрати вираз (невідома помилка): \vec{{A}}_{5}
та Неможливо розібрати вираз (невідома помилка): \vec{{A}}_{6}
, а базис у тривимірному просторі має складатися з трьох одиничних векторів. Ще один одиничний вектор можна дістати, увівши в третє обмеження з
коефіцієнтом +1 штучну змінну х8, якій від-повідатиме одиничний вектор Неможливо розібрати вираз (невідома помилка): \vec{{A}}_{8} = \begin{pmatrix} 0 \\ 0 \\1 \end{pmatrix}
Тепер можемо розглянути розширену задачу лінійного програмування:
На відміну від додаткових змінних штучна змінна х8 має в ці-льовій функції Z коефіцієнт +М (для задачі на min) або –М (для задачі на max), де М — досить велике додатне число.
У розширеній задачі базисними змінними є х5, х6, х8, а решта змінних вільні. Початковий опорний план задачі такий
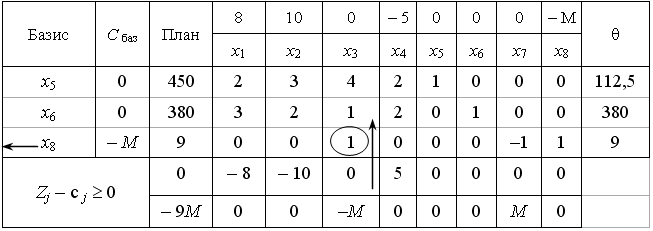
Розраховуючи оцінки першого опорного плану, дістаємо:
Z0 = –9M; Z1 – с1 = –8; Z2 – с2 = –10, Z3 – с3 = –М і т. д. Отже, ми отримуємо оцінки двох видів: одні з них містять М, а інші є звичайними числами. Тому для зручності розділимо оцінковий рядок на два. У перший оцінковий рядок будемо записувати звичайні числа, а в другий — числа з коефіцієнтом М.
Оцінки першого плану не задовольняють умову оптимальності, і тому він є неоптимальним. Виконуємо перехід до наступного опорно-го плану задачі. Після першої ітерації з базису виведена штучна змінна х8. Дальше розв’язування продовжуємо за алгоритмом симплексного методу.
Наступні кроки розв’язування задачі наведені у загальній таблиці:
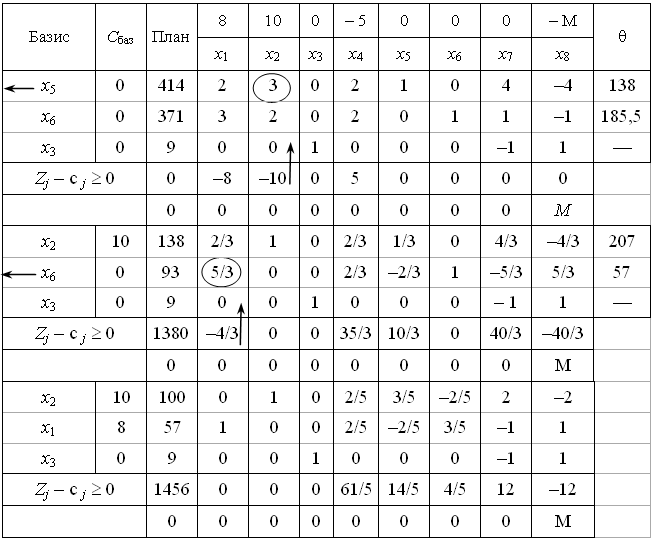
Оптимальним планом задачі є вектор:
