Відмінності між версіями «Перша теорема двоїстості. Економічне тлумачення»
(Створена сторінка: == Перша теорема двоїстості == === Теорема(перша теорема двоїстості) === Якщо одна з пари спря...) |
(→Теорема(перша теорема двоїстості)) |
||
| (не показано 12 проміжних версій цього учасника) | |||
| Рядок 8: | Рядок 8: | ||
Якщо цільова функція однієї із задач необмежена, то спряжена задача також не має розв'язку. | Якщо цільова функція однієї із задач необмежена, то спряжена задача також не має розв'язку. | ||
| − | Зауважимо, що коли одна із задач не має допустимого розв'язку, то двоїста до неї задача також може не мати допустимого розв'язку, тобто зворотне твердження щодо другої частини теореми в загальному випадку не виконується. | + | Зауважимо, що коли одна із задач не має допустимого розв'язку, то двоїста до неї [http://wiki.kspu.kr.ua/index.php/%D0%95%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D1%96%D1%87%D0%BD%D0%B0_%D1%96%D0%BD%D1%82%D0%B5%D1%80%D0%BF%D1%80%D0%B5%D1%82%D0%B0%D1%86%D1%96%D1%8F_%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D1%97_%D1%82%D0%B0_%D0%B4%D0%B2%D0%BE%D1%97%D1%81%D1%82%D0%BE%D1%97_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87_%D0%9B%D0%9F._%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%B0_%D0%BF%D0%BE%D0%B1%D1%83%D0%B4%D0%BE%D0%B2%D0%B8_%D0%B4%D0%B2%D0%BE%D1%97%D1%81%D1%82%D0%B8%D1%85_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87 задача] також може не мати допустимого розв'язку, тобто зворотне твердження щодо другої частини теореми в загальному випадку не виконується. |
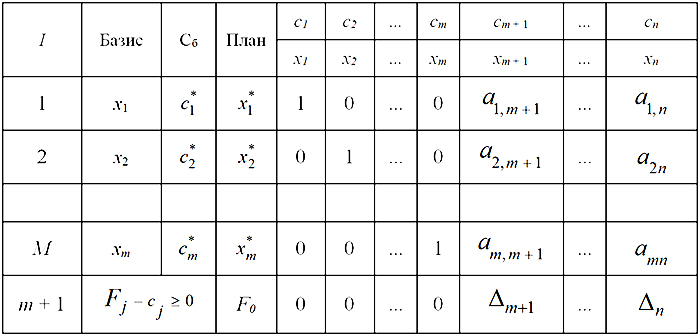
| − | '''''Доведення'''''. Нехай початкова задача має оптимальний план, який отриманий симплексним методом. Не порушуючи загальності, можна вважати, що останній базис складається з перших m векторів <math> A_{1} ,A_{2} ,\dots,A_{m}</math> . Остання симплексна таблиця має вигляд: | + | '''''Доведення'''''. Нехай початкова задача має [http://wiki.kspu.kr.ua/index.php/%D0%A1%D0%B8%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D1%80%D0%BE%D0%B7%D0%B2%E2%80%99%D1%8F%D0%B7%D1%83%D0%B2%D0%B0%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87_%D0%9B%D0%9F._%D0%9E%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%B8%D0%B9_%D1%80%D0%BE%D0%B7%D0%B2%E2%80%99%D1%8F%D0%B7%D0%BE%D0%BA._%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D1%96%D0%B9_%D0%BE%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%96_%D0%BF%D0%BB%D0%B0%D0%BD%D1%83 оптимальний план], який отриманий [http://wiki.kspu.kr.ua/index.php/%D0%A1%D0%B8%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D1%80%D0%BE%D0%B7%D0%B2%E2%80%99%D1%8F%D0%B7%D1%83%D0%B2%D0%B0%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87_%D0%9B%D0%9F._%D0%9F%D0%B5%D1%80%D0%B5%D1%85%D1%96%D0%B4_%D0%B2%D1%96%D0%B4_%D0%BE%D0%B4%D0%BD%D0%BE%D0%B3%D0%BE_%D0%BE%D0%BF%D0%BE%D1%80%D0%BD%D0%BE%D0%B3%D0%BE_%D0%BF%D0%BB%D0%B0%D0%BD%D1%83_%D0%B4%D0%BE_%D1%96%D0%BD%D1%88%D0%BE%D0%B3%D0%BE симплексним методом]. Не порушуючи загальності, можна вважати, що останній базис складається з перших m векторів <math> A_{1} ,A_{2} ,\dots,A_{m}</math> . Остання симплексна таблиця має вигляд: |
| − | |||
| − | + | [[Файл:Simp_dvoist.jpg|center]] | |
| − | Позначимо через D матрицю, що утворена з компонент векторів <math> A_{1} ,A_{2} ,\dots ,A_{m}</math> останнього базису в першій симплексній таблиці. | + | <center>''Таблиця 1''</center> |
| + | Позначимо через <math>D~</math> матрицю, що утворена з компонент векторів <math> A_{1} ,A_{2} ,\dots ,A_{m}</math> останнього базису в першій симплексній таблиці. | ||
Для оптимального плану отримаємо: | Для оптимального плану отримаємо: | ||
| Рядок 22: | Рядок 22: | ||
| − | де <math>X^{*} =(x_{1}^{*} ,x_{2}^{*} ,...,x_{m}^{*} )</math>, <math>\Beta ~</math> | + | де <math>X^{*} =(x_{1}^{*} ,x_{2}^{*} ,...,x_{m}^{*} )</math>, <math>\Beta ~</math> - вектор, що складається з вільних членів системи обмежень. |
Звідси: | Звідси: | ||
| Рядок 28: | Рядок 28: | ||
<center><math> ~ B=DX^{*} \Rightarrow X^{*} =D^{-1} B.~~~~~~~~(2) </math> </center> | <center><math> ~ B=DX^{*} \Rightarrow X^{*} =D^{-1} B.~~~~~~~~(2) </math> </center> | ||
| − | Симплексна таблиця '' | + | Симплексна таблиця ''1'' містить коефіцієнти розкладу векторів <math>~A_{1} ,A_{2} ,...,A_{n}</math> початкової системи обмежень задачі за векторами базису, тобто кожному вектору з системи обмежень задачі <math>~A_{j}</math> відповідає в симплексній таблиці вектор <math>~A'_{j}</math>, такий що |
<center><math>A_{j} =DA'_{j} ,\, \, \, (j=\overline{1,n}).~~~~~~~~(3)</math></center> | <center><math>A_{j} =DA'_{j} ,\, \, \, (j=\overline{1,n}).~~~~~~~~(3)</math></center> | ||
| Рядок 38: | Рядок 38: | ||
звідки | звідки | ||
| − | <center><math>A'_{} =D^{-1} A~~~~~~~~(4)</math> | + | <center><math>A'_{} =D^{-1} A~~~~~~~~(4)</math> </center> |
Враховуючи <math>~(2)</math>, значення оптимального плану даної задачі знаходиться у вигляді: | Враховуючи <math>~(2)</math>, значення оптимального плану даної задачі знаходиться у вигляді: | ||
| Рядок 74: | Рядок 74: | ||
<center><math>Z(Y^{*} )=Y^{*} B=C^{*} D^{-1} B=C^{*} X^{*} =\max \, F.~~~~~~~~(8)</math></center> | <center><math>Z(Y^{*} )=Y^{*} B=C^{*} D^{-1} B=C^{*} X^{*} =\max \, F.~~~~~~~~(8)</math></center> | ||
| − | Доведено, що <math>Z(Y^{*}~ )</math> збігається зі значенням оптимального плану початкової задачі. Отже, за лемою (достатня умова оптимальності плану задачі лінійного програмування) план <math>Y^{*}~</math> є оптимальним планом двоїстої задачі. | + | Доведено, що <math>Z(Y^{*}~ )</math> збігається зі значенням оптимального плану початкової задачі. Отже, за лемою (достатня [http://wiki.kspu.kr.ua/index.php/%D0%A1%D0%B8%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4_%D1%80%D0%BE%D0%B7%D0%B2%E2%80%99%D1%8F%D0%B7%D1%83%D0%B2%D0%B0%D0%BD%D0%BD%D1%8F_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87_%D0%9B%D0%9F._%D0%9E%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%B8%D0%B9_%D1%80%D0%BE%D0%B7%D0%B2%E2%80%99%D1%8F%D0%B7%D0%BE%D0%BA._%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D1%96%D0%B9_%D0%BE%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%96_%D0%BF%D0%BB%D0%B0%D0%BD%D1%83 умова оптимальності плану] задачі лінійного програмування) план <math>Y^{*}~</math> є оптимальним планом двоїстої задачі. |
Аналогічно доводиться, що коли двоїста задача має розв'язок, то початкова також має розв'язок і виконується рівність: | Аналогічно доводиться, що коли двоїста задача має розв'язок, то початкова також має розв'язок і виконується рівність: | ||
| Рядок 83: | Рядок 83: | ||
Доведена теорема дає змогу в процесі розв'язування однієї задачі водночас знаходити план другої. | Доведена теорема дає змогу в процесі розв'язування однієї задачі водночас знаходити план другої. | ||
| − | |||
=== Економічний зміст першої теореми двоїстості. === | === Економічний зміст першої теореми двоїстості. === | ||
| − | Максимальний прибуток <math>( | + | Максимальний прибуток <math>(F_{\max })~</math> підприємство отримує за умови виробництва продукції згідно з оптимальним планом <math>X^{*} =(x_{1}^{*} ,x_{2}^{*} ,...,x_{n}^{*} ),</math> однак таку саму суму грошей <math>(Z_{\min } =F_{\max })~</math> воно може мати, реалізувавши ресурси за оптимальними цінами <math>Y^{*} =(y_{1}^{*} ,y_{2}^{*} ,...,y_{m}^{*} ).</math> За умов використання інших планів <math>X\ne X_{opt} ,\, Y\ne Y_{opt}</math> на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво. |
| + | |||
| + | == Література == | ||
| + | 1.[http://fingal.com.ua/content/view/453/76/1/3/ Математичне програмування - Наконечний С.І. ] <br> | ||
| + | 2.[http://gendocs.ru/v13919/?download=7 Введення в теорію двоїстості (.doc)] | ||
Поточна версія на 11:31, 4 травня 2012
Зміст
Перша теорема двоїстості
Теорема(перша теорема двоїстості)
Якщо одна з пари спряжених задач має оптимальний план, то й друга задача також має розв'язок, причому для оптимальних розв'язків значення цільових функцій обох задач збігаються, тобто
Якщо цільова функція однієї із задач необмежена, то спряжена задача також не має розв'язку.
Зауважимо, що коли одна із задач не має допустимого розв'язку, то двоїста до неї задача також може не мати допустимого розв'язку, тобто зворотне твердження щодо другої частини теореми в загальному випадку не виконується.
Доведення. Нехай початкова задача має оптимальний план, який отриманий симплексним методом. Не порушуючи загальності, можна вважати, що останній базис складається з перших m векторів Неможливо розібрати вираз (невідома помилка): A_{1} ,A_{2} ,\dots,A_{m}
. Остання симплексна таблиця має вигляд:
Позначимо через Неможливо розібрати вираз (невідома помилка): D~
матрицю, що утворена з компонент векторів Неможливо розібрати вираз (невідома помилка): A_{1} ,A_{2} ,\dots ,A_{m}
останнього базису в першій симплексній таблиці.
Для оптимального плану отримаємо:
де Неможливо розібрати вираз (невідома помилка): X^{*} =(x_{1}^{*} ,x_{2}^{*} ,...,x_{m}^{*} )
, Неможливо розібрати вираз (невідома помилка): \Beta ~
- вектор, що складається з вільних членів системи обмежень.
Звідси:
Симплексна таблиця 1 містить коефіцієнти розкладу векторів Неможливо розібрати вираз (невідома помилка): ~A_{1} ,A_{2} ,...,A_{n}
початкової системи обмежень задачі за векторами базису, тобто кожному вектору з системи обмежень задачі Неможливо розібрати вираз (невідома помилка): ~A_{j}
відповідає в симплексній таблиці вектор Неможливо розібрати вираз (невідома помилка): ~A'_{j}
, такий що
Позначимо через Неможливо розібрати вираз (невідома помилка): A'~
матрицю, що складається з коефіцієнтів розкладу векторів Неможливо розібрати вираз (невідома помилка): A_{j}~ \left(j=\overline{1,n}\right)
. Тоді буде справджуватися рівність:
звідки
Враховуючи Неможливо розібрати вираз (невідома помилка): ~(2) , значення оптимального плану даної задачі знаходиться у вигляді:
де Неможливо розібрати вираз (невідома помилка): C^{*} =(c_{1}^{*} ,c_{2}^{*} ,...,c_{m}^{*} ),
причому
тобто всі компоненти вектора Неможливо розібрати вираз (невідома помилка): \bar{F}
є оцінками оптимального плану задачі, а тому
Оскільки оптимальний план початкової задачі подано у вигляді Неможливо розібрати вираз (невідома помилка): X^{*} =D^{-1} B~ , то за правилами побудови двоїстої задачі можна допустити, що її оптимальний план матиме вигляд:
Доведемо, що Неможливо розібрати вираз (невідома помилка): Y^{*} =C^{*} D^{-1}~
дійсно є оптимальним планом двоїстої задачі.
Система обмежень двоїстої задачі у векторно-матричній формі матиме вигляд:
Підставимо в цю нерівність значення Неможливо розібрати вираз (невідома помилка): Y^{*}.~
Тоді, враховуючи Неможливо розібрати вираз (невідома помилка): (4),(5)~ та Неможливо розібрати вираз (невідома помилка): (6)~ отримаємо:
Звідки: Неможливо розібрати вираз (невідома помилка): Y^{*} A\ge C . Отже, Неможливо розібрати вираз (невідома помилка): Y^{*}~
задовольняє систему обмежень Неможливо розібрати вираз (невідома помилка): (4)~ двоїстої задачі, тому є допустимим планом задачі Неможливо розібрати вираз (невідома помилка): (3)-(5)~
. Для даного плану значення функціонала дорівнюватиме:
де Неможливо розібрати вираз (невідома помилка): B=(b_{1} ,b_{2} ,...,b_{m}~ ).
Підставимо в Неможливо розібрати вираз (невідома помилка): (7)~
значення Неможливо розібрати вираз (невідома помилка): Y^{*}~
з Неможливо розібрати вираз (невідома помилка): (6)~
та, враховуючи Неможливо розібрати вираз (невідома помилка): (2)~
, матимемо:
Доведено, що Неможливо розібрати вираз (невідома помилка): Z(Y^{*}~ )
збігається зі значенням оптимального плану початкової задачі. Отже, за лемою (достатня умова оптимальності плану задачі лінійного програмування) план Неможливо розібрати вираз (невідома помилка): Y^{*}~ є оптимальним планом двоїстої задачі.
Аналогічно доводиться, що коли двоїста задача має розв'язок, то початкова також має розв'язок і виконується рівність:
Для доведення другої частини теореми допустимо, що лінійна функція початкової задачі необмежена зверху. Тоді з нерівності Неможливо розібрати вираз (невідома помилка): F(X)\le Z(Y)
маємо, що Неможливо розібрати вираз (невідома помилка): Z(Y)\ge +\infty
, що не має змісту. Отже, двоїста задача в даному разі не має розв'язків.
Доведена теорема дає змогу в процесі розв'язування однієї задачі водночас знаходити план другої.
Економічний зміст першої теореми двоїстості.
Максимальний прибуток Неможливо розібрати вираз (невідома помилка): (F_{\max })~
підприємство отримує за умови виробництва продукції згідно з оптимальним планом Неможливо розібрати вираз (невідома помилка): X^{*} =(x_{1}^{*} ,x_{2}^{*} ,...,x_{n}^{*} ),
однак таку саму суму грошей Неможливо розібрати вираз (невідома помилка): (Z_{\min } =F_{\max })~
воно може мати, реалізувавши ресурси за оптимальними цінами Неможливо розібрати вираз (невідома помилка): Y^{*} =(y_{1}^{*} ,y_{2}^{*} ,...,y_{m}^{*} ).
За умов використання інших планів Неможливо розібрати вираз (невідома помилка): X\ne X_{opt} ,\, Y\ne Y_{opt}
на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво.
Література
1.Математичне програмування - Наконечний С.І.
2.Введення в теорію двоїстості (.doc)