Відмінності між версіями «Сферичні функції Беселя»
Матеріал з Вікі ЦДУ
| (не показано 7 проміжних версій цього учасника) | |||
| Рядок 5: | Рядок 5: | ||
=== Сферичні функції Бесселя: ''j''<sub>''n''</sub>, ''y''<sub>''n''</sub>=== | === Сферичні функції Бесселя: ''j''<sub>''n''</sub>, ''y''<sub>''n''</sub>=== | ||
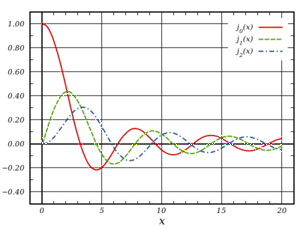
| − | [[Image: | + | [[Image:500px-Spherical_Bessel_j_Functions_(n=0,1,2)1.png|thumb|300px|right|Сферичні функції Бесселя першого роду, ''j''<sub>''n''</sub>(''x''), ''n'' = 0, 1, 2]] |
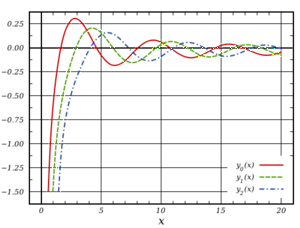
| − | [[Image: | + | [[Image:500px-Spherical_Bessel_y_Functions_(n=0,1,2)23.png|thumb|300px|right|Сферичні функції Бесселя другого роду, ''y''<sub>''n''</sub>(''x''), ''n'' = 0, 1, 2]] |
При розв'язанні [[рівняння Гельмгольца]] в сферичних координатах методом відокремлення змінних, радіальне рівняння має наступний вигляд: | При розв'язанні [[рівняння Гельмгольца]] в сферичних координатах методом відокремлення змінних, радіальне рівняння має наступний вигляд: | ||
:<math>x^2 \frac{d^2 y}{dx^2} + 2x \frac{dy}{dx} + [x^2 - n(n+1)]y = 0.</math> | :<math>x^2 \frac{d^2 y}{dx^2} + 2x \frac{dy}{dx} + [x^2 - n(n+1)]y = 0.</math> | ||
| − | 2 лінійно незалежних розв'язки цього рівняння | + | 2 лінійно незалежних розв'язки цього рівняння називаются '''сферичними функціями Бесселя''' |
''j''<sub>''n''</sub> and ''y''<sub>''n''</sub>, і пов'язані із звичайними функціями Бесселя ''J''<sub>''n''</sub> and ''Y''<sub>''n''</sub> | ''j''<sub>''n''</sub> and ''y''<sub>''n''</sub>, і пов'язані із звичайними функціями Бесселя ''J''<sub>''n''</sub> and ''Y''<sub>''n''</sub> | ||
| Рядок 18: | Рядок 18: | ||
:<math>y_{n}(x) = \sqrt{\frac{\pi}{2x}} Y_{n+1/2}(x) = (-1)^{n+1} \sqrt{\frac{\pi}{2x}} J_{-n-1/2}(x).</math> | :<math>y_{n}(x) = \sqrt{\frac{\pi}{2x}} Y_{n+1/2}(x) = (-1)^{n+1} \sqrt{\frac{\pi}{2x}} J_{-n-1/2}(x).</math> | ||
| − | <math>y_n</math> також позначається <math>n_n</math> або [[Eta (letter)|η]]<sub>n</sub>; Деякі автори називають ці функції | + | <math>y_n</math> також позначається <math>n_n</math> або [[Eta (letter)|η]]<sub>n</sub>; Деякі автори називають ці функції сферичними функціями Неймана. |
| + | |||
| + | Перші кілька сферичних функцій Бесселя: | ||
| + | |||
| + | :<math>j_0(x)=\frac{\sin x} {x}</math> | ||
| + | :<math>j_1(x)=\frac{\sin x} {x^2}- \frac{\cos x} {x}</math> | ||
| + | :<math>j_2(x)=\left(\frac{3} {x^2} - 1 \right)\frac{\sin x}{x} - \frac{3\cos x} {x^2}</math> | ||
| + | :<math>j_3(x)=\left(\frac{15}{x^3} - \frac{6}{x} \right)\frac{\sin x}{x} -\left(\frac{15}{x^2} - 1\right) \frac{\cos x} {x},</math> | ||
| + | та | ||
| + | :<math>y_0(x)=-j_{-1}(x)=-\,\frac{\cos x} {x}</math> | ||
| + | :<math>y_1(x)=j_{-2}(x)=-\,\frac{\cos x} {x^2}- \frac{\sin x} {x}</math> | ||
| + | :<math>y_2(x)=-j_{-3}(x)=\left(-\,\frac{3}{x^2}+1 \right)\frac{\cos x}{x}- \frac{3 \sin x} {x^2};</math> | ||
| + | |||
| + | :<math>J_{n+\frac 1 2}(x)=\sqrt \frac 2 {\pi x} \sum_{i=0}^\frac {n+1} 2 (-1)^{n-i}\left[\sin(x) \left(\frac 2 x\right)^{n-2i} \frac {(n-i)!}{i!} {-\frac 1 2-i \choose n-2i}- \cos(x) \left(\frac 2 x\right)^{n+1-2i} \frac {(n-i)!}{i!} i {-\frac 1 2-i \choose n-2i+1}\right].</math> | ||
| + | |||
| + | Виконала: [[Користувач: Куян Юлія Іванівна|Куян Юлія]] | ||
| + | |||
| + | [[category: Вибрані статті з математичного аналізу]] | ||
Поточна версія на 21:40, 20 травня 2010
Функції Бесселя в математиці - сім'я функцій, які є канонічними розв'язками диференціального рівняння Бесселя:
- Неможливо розібрати вираз (невідома помилка): x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0,
де Неможливо розібрати вираз (невідома помилка): \alpha
— довільне дійсне число, яке називається порядком.
Сферичні функції Бесселя: jn, yn
При розв'язанні рівняння Гельмгольца в сферичних координатах методом відокремлення змінних, радіальне рівняння має наступний вигляд:
- Неможливо розібрати вираз (невідома помилка): x^2 \frac{d^2 y}{dx^2} + 2x \frac{dy}{dx} + [x^2 - n(n+1)]y = 0.
2 лінійно незалежних розв'язки цього рівняння називаются сферичними функціями Бесселя
jn and yn, і пов'язані із звичайними функціями Бесселя Jn and Yn
- Неможливо розібрати вираз (невідома помилка): j_{n}(x) = \sqrt{\frac{\pi}{2x}} J_{n+1/2}(x),
- Неможливо розібрати вираз (невідома помилка): y_{n}(x) = \sqrt{\frac{\pi}{2x}} Y_{n+1/2}(x) = (-1)^{n+1} \sqrt{\frac{\pi}{2x}} J_{-n-1/2}(x).
Неможливо розібрати вираз (невідома помилка): y_n
також позначається Неможливо розібрати вираз (невідома помилка): n_n або ηn; Деякі автори називають ці функції сферичними функціями Неймана.
Перші кілька сферичних функцій Бесселя:
- Неможливо розібрати вираз (невідома помилка): j_0(x)=\frac{\sin x} {x}
- Неможливо розібрати вираз (невідома помилка): j_1(x)=\frac{\sin x} {x^2}- \frac{\cos x} {x}
- Неможливо розібрати вираз (невідома помилка): j_2(x)=\left(\frac{3} {x^2} - 1 \right)\frac{\sin x}{x} - \frac{3\cos x} {x^2}
- Неможливо розібрати вираз (невідома помилка): j_3(x)=\left(\frac{15}{x^3} - \frac{6}{x} \right)\frac{\sin x}{x} -\left(\frac{15}{x^2} - 1\right) \frac{\cos x} {x},
та
- Неможливо розібрати вираз (невідома помилка): y_0(x)=-j_{-1}(x)=-\,\frac{\cos x} {x}
- Неможливо розібрати вираз (невідома помилка): y_1(x)=j_{-2}(x)=-\,\frac{\cos x} {x^2}- \frac{\sin x} {x}
- Неможливо розібрати вираз (невідома помилка): y_2(x)=-j_{-3}(x)=\left(-\,\frac{3}{x^2}+1 \right)\frac{\cos x}{x}- \frac{3 \sin x} {x^2};
- Неможливо розібрати вираз (невідома помилка): J_{n+\frac 1 2}(x)=\sqrt \frac 2 {\pi x} \sum_{i=0}^\frac {n+1} 2 (-1)^{n-i}\left[\sin(x) \left(\frac 2 x\right)^{n-2i} \frac {(n-i)!}{i!} {-\frac 1 2-i \choose n-2i}- \cos(x) \left(\frac 2 x\right)^{n+1-2i} \frac {(n-i)!}{i!} i {-\frac 1 2-i \choose n-2i+1}\right].
Виконала: Куян Юлія