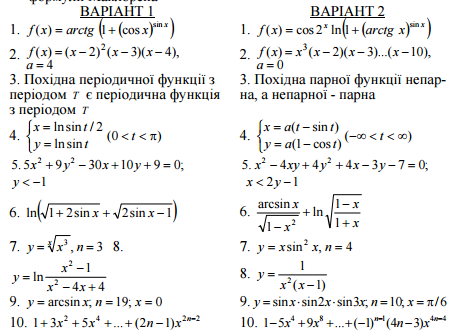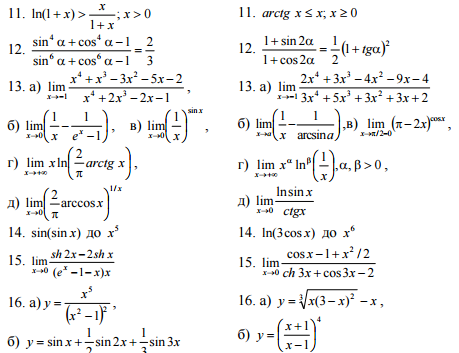Відмінності між версіями «Дистанційний курс з математичного аналізу»

Матеріал з Вікі ЦДУ
Перейти до: навігація, пошук
(Створена сторінка: =Назва курсу= ...... ---- Галузь знань, напрям підготовки, освітньо-кваліфікаційний рівень:...)
 
 
(не показані 4 проміжні версії цього учасника)
Рядок 1: Рядок 1:
 
=Назва курсу=
 
=Назва курсу=
−
......
+
<p style="text-align:center"><font face ="Times New Roman" color="red" size="13">Математичний аналіз. Диференціальне числення функції однієї змінної</font>
 +
</p>
 
----  
 
----  
−
Галузь знань, напрям підготовки, освітньо-кваліфікаційний рівень:
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">Галузь знань, напрям підготовки, освітньо-кваліфікаційний рівень: 0402 фізико-математичні науки. Напрям підготовки 6.040201 Математика*</font>
 +
</p>
  
 
==Мета та завдання навчального курсу==
 
==Мета та завдання навчального курсу==
−
Мета ..............
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">Мета: закласти фундамент математичної підготовки майбутнього вчителя математики; підготувати студентів до вивчення курсів загальної та теоретичної фізики, диференціальних рівнянь та комплексного аналізу.
 +
</font>
 +
</p>
  
−
Завдання .....................
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">Завдання вивчення дисципліни: навчити студентів основним поняттям диференціального та інтегрального числення, метричних просторів, функції кількох змінних; навчити студентів доводити основні теореми вказаних розділів; навчити студентів застосовувати поняття і теореми математичного аналізу до дослідження функцій, обчислення довжин кривих, площ поверхонь, моментів інерції та статичних моментів, знаходження кратних і контурних інтегралів.
 +
</font>
 +
</p>
  
−
У результаті вивчення навчального курсу студент повинен
 
  
−
знати: ....................
 
  
−
вміти: ...................
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">У результаті вивчення навчального курсу студент повинен
 +
</font>
 +
</p>
  
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">знати: історію розвитку математичного апарату математичного аналізу; властивості елементарних функцій; теорію меж та нескінченно малих величин; похідну та диференціал функції однієї і декількох змінних та їхнє застосування; інтегральне числення; числові та. функціональні ряди; основи диференціальних рівнянь;
  
−
[http://www.example.com Робоча програма курсу]
+
</font>
−
==Автор (автори) курсу==
+
</p>
−
Посилання на сторінки авторів
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">вміти: виконувати операції над множинами; обчислювати границі послідовностей; досліджувати функції на неперервність; обчислювати похідну функції; досліджувати функції за допомогою похідних; обчислювати невизначені інтеграли; обчислювати похідні за напрямком і частинні похідні; застосовувати диференціал функції до наближених обчислень; знаходити похідні та диференціали вищих порядків; користуватися правилом Лопіталя; застосовувати теореми Ролля, Лагранжа та Коші; знаходити опуклість кривої та точки перегину; досліджувати та будувати графіки функцій;
 +
</font>
 +
</p>
  
−
----
+
==Автор курсу==
−
=Учасники=
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">Великоіваненко Сергій Вадимович</font>
−
[[Сторінка координування курсу "Сучасні інформаційні технології"]] викладач [[Користувач:Андронатій Павло Іванович|Андронатій Павло Іванович]]
+
</p>
  
  
−
----
+
==Структура ==
  
−
=Графік навчання=
+
===Змістовий модуль: Диференціальне числення функції однієї змінної===
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">Теми: Диференціальне числення.
 +
Основні теореми диференціального числення</font>
 +
</p>
  
−
==Варіант Структура ==
+
==Календар==
  
−
===Змістовий модуль 1===
+
===Тиждень 1===
−
Навчальні теми змістового модуля 1.
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">1. Задачі, що проводять до поняття похідної. Означення похідної.  Механічний та геометричний зміст похідної.</font>
 +
</p>
  
−
===Змістовий модуль 2===
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">2. Односторонні похідні. Нескінченні похідні.</font>
−
Навчальні теми змістового модуля 2.
+
</p>
  
−
===Змістовий модуль 3===
 
−
Навчальні теми змістового модуля 3.
 
  
−
===Змістовий модуль 4===
+
===Тиждень 2===
−
Навчальні теми змістового модуля 4.
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">1. Диференційовність функції. Похідні елементарних функцій. Похідна оберненої функції.</font>
 +
</p>
  
−
==Варіант Календар==
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">2. Диференціал функції. Похідні вищих порядків. Диференціали вищих порядків. </font>
 +
</p>
  
−
===Тиждень 1===
 
−
Навчальні теми для вивчення на  1-му тижні.
 
  
−
===Тиждень 2===
+
===Тиждень 3===
−
Навчальні теми для вивчення на  2-му тижні.
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">1. Теореми про середнє значення. Теорема Ферма. Теорема Ролля.</font>
 +
</p>
 +
 
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">2. Теорема Лагранжа. Теорема Коші.</font>
 +
</p>
 +
 
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">3. Розкриття невизначеностей. Правило Лопіталя. Застосування правила Лопіталя при розкритті невизначеностей </font>
 +
</p>
  
−
===Тиждень 3===
 
−
Навчальні теми для вивчення на  3-му тижні.
 
  
 
===Тиждень 4===
 
===Тиждень 4===
−
Навчальні теми для вивчення на 4-му тижні.
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">1. Ознака монотонності функції. Екстремальні точки.</font>
 +
</p>
 +
 
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">2. Необхідні й достатні умови існування екстремуми функції. </font>
 +
</p>
 +
Знаходження найбільшого й найменшого значення функції на відрізку.
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">3. Опуклість та вгнутість кривої. Точки перегину. Асимптоти графіка функції. Загальна схема дослідження функцій і побудови їх графіків.</font>
 +
</p>
  
 
----
 
----
  
 
=Зміст курсу=
 
=Зміст курсу=
−
==Змістовий модуль І. Назва модулю==
+
==Змістовий модуль. Диференціальне числення функції однієї змінної==
−
===Тема 1. Назва теми===
+
===Тема 1. Дифренціальне числення===
 
====Теоретичний матеріал====
 
====Теоретичний матеріал====
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №1]
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMRDcxSm1JUlMyTUU/view?usp=sharing Лекція №1 Задачі, що проводять до поняття похідної. Означення похідної.  Механічний та геометричний зміст похідної.]
  
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №2]
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMZlpreEJsTUdpM2c/view?usp=sharing Лекція №2 Односторонні похідні. Нескінченні похідні.]  
  
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №3]
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMUTFST3RWM01jN0k/view?usp=sharing Лекція №3 Диференційовність функції. Похідні елементарних функцій. Похідна оберненої функції.]
  
 +
[https://drive.google.com/file/d/0B-YSyZTsDzVMelA4OERsQmZ3dWs/view?usp=sharing Лекція №4 Диференціал функції. Похідні вищих порядків. Диференціали вищих порядків.]
 
====Практичні завдання====
 
====Практичні завдання====
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Практична №1]
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Практична №1]
Рядок 80: Рядок 104:
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Самостійна  робота №2]
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Самостійна  робота №2]
  
−
==Змістовий модуль ІІ. Назва модулю==
+
===Тема 2. Основні теореми диференціального числення ===
−
===Тема 1. Назва теми===
+
 
====Теоретичний матеріал====
 
====Теоретичний матеріал====
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №1]
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMaEYxUGwzV3pzbFk/view?usp=sharing Лекція №1 Теореми про середнє значення. Теорема Ферма. Теорема Ролля.]
  
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №2]
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMOFQ0TFlBT3VaOVU/view?usp=sharing Лекція №2 Теорема Лагранжа. Теорема Коші.]
  
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №3]
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMNGNFTjF6aHlzNWM/view?usp=sharing Лекція №3 Розкриття невизначеностей. Правило Лопіталя. Застосування правила Лопіталя при розкритті невизначеностей ]
  
−
====Практичні завдання====
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMdDc0TmVSRlFsYm8/view?usp=sharing Лекція №4 Ознака монотонності функції. Екстремальні точки.]
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Практична №1]
+
−
 
+
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Практична №2]
+
−
 
+
−
====Самостійна робота====
+
−
 
+
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Самостійна робота №1]
+
−
 
+
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Самостійна  робота №2]
+
−
 
+
−
==Змістовий модуль ІІІ. Назва модулю==
+
−
===Тема 1. Назва теми===
+
−
====Теоретичний матеріал====
+
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №1]
+
−
 
+
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №2]
+
  
−
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Лекція №3]
+
[https://drive.google.com/file/d/0B-YSyZTsDzVMdDc0TmVSRlFsYm8/view?usp=sharing Лекція №5 Необхідні й достатні умови існування екстремуми функції. Знаходження найбільшого й найменшого значення функції на відрізку]
  
 +
[https://drive.google.com/file/d/0B-YSyZTsDzVMNzRBQjdieERDSEk/view?usp=sharing Лекція №6 Опуклість та вгнутість кривої. Точки перегину. Асимптоти графіка функції. Загальна схема дослідження функцій і побудови їх графіків.]
 
====Практичні завдання====
 
====Практичні завдання====
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Практична №1]
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Практична №1]
Рядок 120: Рядок 128:
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Самостійна  робота №2]
 
[https://owncloud.kspu.kr.ua/index.php/s/6RpYzTdWTbgF97g Самостійна  робота №2]
  
 +
====Індивідуальна робота====
 +
[[Файл:Screenshot 12.png|Умови]]
 +
[[Файл:Screenshot 10.png|Завдання]]
 +
[[Файл:Screenshot 11.png|Завдання]]
 
----
 
----
  
Рядок 125: Рядок 137:
 
==Рекомендована література==
 
==Рекомендована література==
 
===Базова===
 
===Базова===
−
#
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">1.Шкіль М.І. Математичний аналіз. Ч. І. — K.: Вища школа. 2005,1978.</font>
−
#
+
</p>
−
#
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">2.Шкіль М.І. Математичний аналіз. 4.2. — K.: Вища школа, 2005.</font>
−
 
+
</p>
−
 
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">3.Давидов М.О. Курс математичного аналізу. Ч. І. K.: Вища школа. 1976,1990.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">4.А. Давидов М.О. Курс математичного аналізу. Ч. II. - K.: Вища школа. 1976, 1990</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">5.Будак Б.М., Фомин C.B. Кратные интегралы и ряды. - Москва: Наука. 1967.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">6.Колмогоров А.М, Фомин С.В. Елементи теорії функцій і функціонального аналізу. — K.: Вища школа, 1974.</font>
 +
</p>
 
===Допоміжна===
 
===Допоміжна===
−
#
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">1.Романов В.А., Вороной А.Н. Метрические пространства. - Кировоград: Изд-во «Кіровоградська правда», 1980.</font>
−
#
+
</p>
−
#
+
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">2.Романов В. О. Функціональний аналіз. - Кіровоград: РВЦ КДПУ ім. В.Винниченка, 2003.</font>
−
 
+
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">3.Дзядик В.К. Математичний аналіз. Т. І. - K.: Вища школа. 1995.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">4.Дороговцев А.Я. Математичний аналіз. Ч. І. - K.: Либідь. 1993.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">5.Дюженкова Л.І., Колесник Т.В., Лященко М.Я., Михалін Г.О., Математичний аналіз у задачах і прикладах. Ч. І.- K.: Вища школа. 2002.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">6.Кудрявцев Л.Д. Математический анализ. Ч. ІІ. - М.: Просвещение. 1970.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">7.Ляшко И.И., Боярчук А.К. и др. Математический анализ в примерах и задачах. Т. 1. - К.: Вища школа. 1974.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">8.Ляшко И.И., Боярчук А.К. и др. Справочное пособие по математическому анализу. - К.: Вища школа. 1984.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">9.Фихтенгольц Г. М. Основы математического анализа. Т.1. Т.2. - М.: Наука. 1968.</font>
 +
</p>
 +
<p style="text-align:left"><font face ="Times New Roman" color="black" size="5">10. М.Н. Шунда, A.A. Томусяк. Практикум з математичного аналізу: Інтегральне числення. Ряди.: Навч. посібник. К. - “Вища шк.”, 1995.</font>
 +
</p>
 
==Інформаційні ресурси==
 
==Інформаційні ресурси==
  
−
#
+
[http://test-trainer.com.ua/ Корисний тренажер для запам'ятовування формул]
−
#
+
[http://sites.znu.edu.ua/bank/public_files/2009/10/matanaliz/metod_Dif_ischesl.pdf Навчальний посібник для студентів першого курсу]
 +
[http://schoolsite.org.ua/4/media/editors/tinymce/upload-files/MetodMA1.pdf Завдання з теми "Диференціальне числення ]
  
 
---
 
---
 
[[Категорія:Навчальні курси]]
 
[[Категорія:Навчальні курси]]

Поточна версія на 08:12, 26 червня 2015

Назва курсу

Математичний аналіз. Диференціальне числення функції однієї змінної

Галузь знань, напрям підготовки, освітньо-кваліфікаційний рівень: 0402 фізико-математичні науки. Напрям підготовки 6.040201 Математика*

Мета та завдання навчального курсу

Мета: закласти фундамент математичної підготовки майбутнього вчителя математики; підготувати студентів до вивчення курсів загальної та теоретичної фізики, диференціальних рівнянь та комплексного аналізу.

Завдання вивчення дисципліни: навчити студентів основним поняттям диференціального та інтегрального числення, метричних просторів, функції кількох змінних; навчити студентів доводити основні теореми вказаних розділів; навчити студентів застосовувати поняття і теореми математичного аналізу до дослідження функцій, обчислення довжин кривих, площ поверхонь, моментів інерції та статичних моментів, знаходження кратних і контурних інтегралів.


У результаті вивчення навчального курсу студент повинен

знати: історію розвитку математичного апарату математичного аналізу; властивості елементарних функцій; теорію меж та нескінченно малих величин; похідну та диференціал функції однієї і декількох змінних та їхнє застосування; інтегральне числення; числові та. функціональні ряди; основи диференціальних рівнянь;

вміти: виконувати операції над множинами; обчислювати границі послідовностей; досліджувати функції на неперервність; обчислювати похідну функції; досліджувати функції за допомогою похідних; обчислювати невизначені інтеграли; обчислювати похідні за напрямком і частинні похідні; застосовувати диференціал функції до наближених обчислень; знаходити похідні та диференціали вищих порядків; користуватися правилом Лопіталя; застосовувати теореми Ролля, Лагранжа та Коші; знаходити опуклість кривої та точки перегину; досліджувати та будувати графіки функцій;

Автор курсу

Великоіваненко Сергій Вадимович


Структура

Змістовий модуль: Диференціальне числення функції однієї змінної

Теми: Диференціальне числення. Основні теореми диференціального числення

Календар

Тиждень 1

1. Задачі, що проводять до поняття похідної. Означення похідної. Механічний та геометричний зміст похідної.

2. Односторонні похідні. Нескінченні похідні.


Тиждень 2

1. Диференційовність функції. Похідні елементарних функцій. Похідна оберненої функції.

2. Диференціал функції. Похідні вищих порядків. Диференціали вищих порядків.


Тиждень 3

1. Теореми про середнє значення. Теорема Ферма. Теорема Ролля.

2. Теорема Лагранжа. Теорема Коші.

3. Розкриття невизначеностей. Правило Лопіталя. Застосування правила Лопіталя при розкритті невизначеностей


Тиждень 4

1. Ознака монотонності функції. Екстремальні точки.

2. Необхідні й достатні умови існування екстремуми функції.

Знаходження найбільшого й найменшого значення функції на відрізку.

3. Опуклість та вгнутість кривої. Точки перегину. Асимптоти графіка функції. Загальна схема дослідження функцій і побудови їх графіків.

Зміст курсу

Змістовий модуль. Диференціальне числення функції однієї змінної

Тема 1. Дифренціальне числення

Теоретичний матеріал

Лекція №1 Задачі, що проводять до поняття похідної. Означення похідної. Механічний та геометричний зміст похідної.

Лекція №2 Односторонні похідні. Нескінченні похідні.

Лекція №3 Диференційовність функції. Похідні елементарних функцій. Похідна оберненої функції.

Лекція №4 Диференціал функції. Похідні вищих порядків. Диференціали вищих порядків.

Практичні завдання

Практична №1

Практична №2

Самостійна робота

Самостійна робота №1

Самостійна робота №2

Тема 2. Основні теореми диференціального числення

Теоретичний матеріал

Лекція №1 Теореми про середнє значення. Теорема Ферма. Теорема Ролля.

Лекція №2 Теорема Лагранжа. Теорема Коші.

Лекція №3 Розкриття невизначеностей. Правило Лопіталя. Застосування правила Лопіталя при розкритті невизначеностей

Лекція №4 Ознака монотонності функції. Екстремальні точки.

Лекція №5 Необхідні й достатні умови існування екстремуми функції. Знаходження найбільшого й найменшого значення функції на відрізку

Лекція №6 Опуклість та вгнутість кривої. Точки перегину. Асимптоти графіка функції. Загальна схема дослідження функцій і побудови їх графіків.

Практичні завдання

Практична №1

Практична №2

Самостійна робота

Самостійна робота №1

Самостійна робота №2

Індивідуальна робота

Умови Завдання Завдання

Ресурси

Рекомендована література

Базова

1.Шкіль М.І. Математичний аналіз. Ч. І. — K.: Вища школа. 2005,1978.

2.Шкіль М.І. Математичний аналіз. 4.2. — K.: Вища школа, 2005.

3.Давидов М.О. Курс математичного аналізу. Ч. І. K.: Вища школа. 1976,1990.

4.А. Давидов М.О. Курс математичного аналізу. Ч. II. - K.: Вища школа. 1976, 1990

5.Будак Б.М., Фомин C.B. Кратные интегралы и ряды. - Москва: Наука. 1967.

6.Колмогоров А.М, Фомин С.В. Елементи теорії функцій і функціонального аналізу. — K.: Вища школа, 1974.

Допоміжна

1.Романов В.А., Вороной А.Н. Метрические пространства. - Кировоград: Изд-во «Кіровоградська правда», 1980.

2.Романов В. О. Функціональний аналіз. - Кіровоград: РВЦ КДПУ ім. В.Винниченка, 2003.

3.Дзядик В.К. Математичний аналіз. Т. І. - K.: Вища школа. 1995.

4.Дороговцев А.Я. Математичний аналіз. Ч. І. - K.: Либідь. 1993.

5.Дюженкова Л.І., Колесник Т.В., Лященко М.Я., Михалін Г.О., Математичний аналіз у задачах і прикладах. Ч. І.- K.: Вища школа. 2002.

6.Кудрявцев Л.Д. Математический анализ. Ч. ІІ. - М.: Просвещение. 1970.

7.Ляшко И.И., Боярчук А.К. и др. Математический анализ в примерах и задачах. Т. 1. - К.: Вища школа. 1974.

8.Ляшко И.И., Боярчук А.К. и др. Справочное пособие по математическому анализу. - К.: Вища школа. 1984.

9.Фихтенгольц Г. М. Основы математического анализа. Т.1. Т.2. - М.: Наука. 1968.

10. М.Н. Шунда, A.A. Томусяк. Практикум з математичного аналізу: Інтегральне числення. Ряди.: Навч. посібник. К. - “Вища шк.”, 1995.

Інформаційні ресурси

Корисний тренажер для запам'ятовування формул Навчальний посібник для студентів першого курсу Завдання з теми "Диференціальне числення

---

Отримано з https://wiki.cusu.edu.ua/index.php?title=Дистанційний_курс_з_математичного_аналізу&oldid=182677