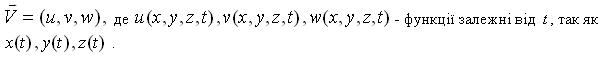Відмінності між версіями «Динамічне рівняння руху у формі Ойлера (Ейлера)»
(Створена сторінка: category:Теорія систем та математичне моделювання) |
|||
| (не показані 2 проміжні версії цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
| + | '''''Метод Ойлера''''' – це локальний метод вивчення суцільного середовища, при якому в просторі виділяється елементарний об’єм як каркас, а рух рідини розглядається через нього.<br> | ||
| + | Об’єктами дослідження є:<bR> | ||
| + | • векторне поле швидкостей;<br> | ||
| + | • векторне поле прискорень;<br> | ||
| + | • поле тиску (скалярне).<br> | ||
| + | Вивчається зміна різних елементів руху у фіксованій точці простору із зміною часу, а також зміна елементів руху при переході до інших точок простору.<br> | ||
| + | [[Файл:Oiler1.JPG]]<br> | ||
| + | ''Зауваження:'' Якщо зафіксувати координати x, y, z то можна отримати динамічну картину в фіксованій точці (відео). Якщо ж зафіксувати t, а x, y, z розглядати як змінні, то отримаємо миттєве фото для всього об’єму суцільного середовища.<br> | ||
| + | [[Файл:Oiler2.JPG]]<br> | ||
| + | (1) - Динамічна система рівнянь у формі Ойлера. Тут x, y, z, t - незалежні змінні; u, v, w, p - невідомі функції. Ця система неповна, оскільки кількість невідомих функцій більша за кількість рівнянь.<br> | ||
| + | [[Файл:Oiler3.JPG]]<br> | ||
| + | |||
| + | |||
[[category:Теорія систем та математичне моделювання]] | [[category:Теорія систем та математичне моделювання]] | ||
Поточна версія на 00:33, 5 червня 2009
Метод Ойлера – це локальний метод вивчення суцільного середовища, при якому в просторі виділяється елементарний об’єм як каркас, а рух рідини розглядається через нього.
Об’єктами дослідження є:
• векторне поле швидкостей;
• векторне поле прискорень;
• поле тиску (скалярне).
Вивчається зміна різних елементів руху у фіксованій точці простору із зміною часу, а також зміна елементів руху при переході до інших точок простору.
Зауваження: Якщо зафіксувати координати x, y, z то можна отримати динамічну картину в фіксованій точці (відео). Якщо ж зафіксувати t, а x, y, z розглядати як змінні, то отримаємо миттєве фото для всього об’єму суцільного середовища.
(1) - Динамічна система рівнянь у формі Ойлера. Тут x, y, z, t - незалежні змінні; u, v, w, p - невідомі функції. Ця система неповна, оскільки кількість невідомих функцій більша за кількість рівнянь.